A Teoria dos Jogos é aclamada como um revolucionário fenômeno interdisciplinar, mesclando conceitos de economia, psicologia, matemática, filosofia e uma miríade de outras áreas acadêmicas. Oito Prêmios Nobel já foram concedidos àqueles que deram contribuições inovadoras para o assunto; todavia, além das fronteiras do mundo acadêmico, a Teoria dos Jogos é realmente aplicável ao mundo corporativo?
Sim! A formalização de estratégias a serem adotadas por empresas em um ambiente de competição é imensamente facilitada quando empregamos os diversos conceitos formulados na Teorias dos Jogos. A análise originada nessa teoria pode nos ajudar a antever as possíveis reações dos agentes a uma dada política econômica – como foi o caso do Plano Cruzado, em 1986, ou do Plano Real, em 1994 -, ou analisar a viabilidade de acordos comerciais, – como o da Organização dos Países Produtores de Petróleo (OPEP), que no início dos anos 1970 decuplicou o preço do barril de petróleo
Um dos exemplos clássicos da Teoria dos Jogos no mundo dos negócios aparece quando analisamos um ambiente econômico caracterizado pelo oligopólio – mercados constituídos por pequeno número de firmas, as quais possuem relativo poder de mercado para estabelecer os preços e quantidades de seus produtos – pois aqui a necessidade de se adotar um comportamento de natureza estratégica é vital para a sobrevivência da empresa no mercado.
A despeito de ser de interesse comum a cooperação com os outros competidores, – pois assim haveria a garantia de preços mais altos, e consequentemente, maiores lucros para todas as firmas no mercado – há o incentivo para que a empresa não participe de conluios, já que esse tipo de acordo, além de suas restrições legais, ainda implica em custos com o monitoramento das outras firmas, que podem estar quebrando o acordo para tentar obter uma maior participação no mercado. Em função disso, as firmas oligopolistas têm enormes incentivos para optar por maximizar seus lucros sem fazer uso de acordos com as outras firmas no mercado, resultando em comportamentos estratégicos capazes de lhes proporcionar uma vantagem competitiva frente a seus concorrentes.
A Teoria dos Jogos tem expandido suas aplicações a outras áreas: de estratégias de campanhas de marketing até negociações salariais, táticas de lances em um leilão e sistemas de votação, ela fornece uma estrutura de hipóteses capaz de conduzir os tomadores de decisão a escolhas eficientes e fundamentadas
Alguns exemplos que podem ser dados: Uma companhia farmacêutica deve decidir se comercializa um novo remédio imediatamente, obtendo uma vantagem competitiva sobre as firmas rivais, ou prolonga o período de teste da nova droga; uma firma em processo falimentar está sendo liquidada e seus ativos estão sendo leiloados, qual deve ser a abordagem correta para esse leilão? Se proprietários de veículos não consideram o custo coletivo do uso de seus carros, que estratégia deve ser adotada pelo poder público para que o custo dos congestionamentos gerados possa ser transferido para cada motorista de modo a desincentivar-lo a usar seu automóvel? Essas e outras inúmeras questões podem ser respondidas através da racionalidade empregada na Teoria dos Jogos.
Dentre as situações que podem ser analisadas com o auxílio dessa Teoria, há algumas em que nossas decisões não podem ser tomadas unilateralmente, isto é, decisões em que nossa conduta depende do que o outro a gente está fazendo. Para entender melhor essa ideia temos que dominar alguns conceitos sobre a tomada de decisão analisada com conceitos de Teoria dos Jogos, e o primeiro deles é o de Estratégias Dominantes.
Teoria dos Jogos – Estratégias Dominantes
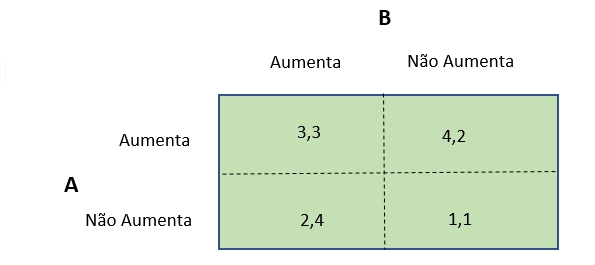
Suponha que dois fabricantes de sabão em pó estejam decidindo sobre a melhor forma de realizar suas campanhas publicitárias. A decisão é sobre se deve haver um aumento de gastos com publicidade ou se se mantém os gastos do ano anterior. A matriz de ganhos – ou de pay off – nos informa os resultados das estratégias adotadas pelas firmas:
A matriz de ganho acima mostra o crescimento porcentual de vendas nos casos de aumento ou não aumento de gastos com publicidade. Quando uma das empresas aumenta seu investimento em propaganda, ela sempre tem um desempenho de vendas melhor do que se não tivesse investido. No caso da empresa A, – cujo ganho está representado pelo primeiro valor em cada uma das quatro células -, se ela aumenta os gastos e a empresa B não, seu crescimento de vendas é de 4% ao invés de 1%; no caso de B também aumentar seus gastos com publicidade, os ganhos de A são de 3%, aumentando os gastos, ao invés de 2%, sem esse aumento. Como a matriz é simétrica, tudo o que foi dito para A é válido para B. Podemos facilmente perceber que é sempre melhor para ambas as firmas aumentar o gasto com publicidade, independente do que esteja sendo feito pelo concorrente.
A situação em que a estratégia adotada pelo jogador independe da estratégia escolhida pelo outro jogador é chamada de Estratégia Dominante, e conduz o jogo a um equilíbrio estável.
Um outro tipo de equilíbrio em Teoria dos Jogos é baseado na premissa de que cada um dos jogadores está adotando a melhor estratégia possível considerando o que o outro jogador está fazendo. Para entender melhor essa ideia usaremos o exemplo do Dilema dos Prisioneiros[1]
A situação descrita no problema é sobre o interrogatório de dois assaltantes, os quais roubaram um banco e agora são mantidos em celas distintas, sem chances de estabelecer qualquer tipo de comunicação entre si. A eles são dadas as seguintes opções:
- Caso um dos assaltantes confesse o crime e o outro não, aquele que confessou irá ser punido com apenas um ano de prisão, enquanto o assaltante que optou por não confessar será condenado a dez anos na cadeia;
- Se os dois não confessarem, a condenação será de dois anos para ambos;
- E se os dois confessarem, a pena irá para cinco anos
Conforme podemos observar, os prisioneiros estão impossibilitados de estabelecer qualquer tipo de acordo, e considerando a ausência de informações sobre como cada um irá se comportar em relação aos incentivos apresentados, eles acabam por confessar o crime[2]. Vejamos a matriz de ganhos abaixo para compreender o porquê disso:
Confessar o crime é sempre a melhor estratégia. Se o prisioneiro 1 confessar, e o outro não, o confessor é condenado a um ano ao invés de dois anos; caso o prisioneiro 2 também confesse, a superioridade da confissão também se verifica, pois aqui o prisioneiro 1 é condenado a 5 anos ao invés de 10.
O Dilema dos Prisioneiros representa situações em que os participantes de um jogo estariam em melhor situação, se pudessem estabelecer um acordo entre si, mas não conseguem concretizá-lo por conta de algumas impossibilidades, tais como, elevados custos de monitoramento dos participantes para que esses cumpram sua parte no acordo, ou a existência de incentivos para o descumprimento do trato. A formação de cartéis é um típico caso de Dilema dos Prisioneiros, pois além de ser difícil monitorar o comportamento das empresas que aderiram ao cartel, o crescimento dos lucros decorrentes do acordo aumentam os incentivos para que cada membro do cartel tente expandir sua participação no mercado através da redução do preço praticado.
Teoria dos Jogos – Equilíbrio de Nash
Vimos que a natureza do equilíbrio do jogo representado pelo Dilema dos Prisioneiros guarda uma importante diferença em relação ao conceito de estratégia dominante. Enquanto nesta última o participante do jogo pode escolher sua estratégia sem considerar o que seu oponente está fazendo, no Dilema dos Prisioneiros, o jogador não pode negligenciar as escolhas do outro, sob pena de poder obter um resultado extremamente negativo. Esse novo tipo de equilíbrio foi nomeado Equilíbrio de Nash, em honra a John Forbes Nash (1928 -2015), – matemático norte-americano que recebeu o prêmio Nobel de economia em 1994 por suas contribuições à teoria dos jogos.
O Equilíbrio de Nash pode ser entendido como o resultado da interação entre dois agentes que estão fazendo as melhores escolhas possíveis em relação ao que o outro jogador está fazendo. Equilíbrios de Nash são comuns em diversas situações de interação estratégica, tanto no nível de empresas de pequeno porte, quanto na escala de grandes economias como EUA e China (a atual política protecionista do Governo Trump está ensejando uma reação de Pequim que caracteriza bem o conceito de Equilíbrio de Nash)
O caso citado da política comercial do Governo Trump é de interesse especial pelo fato de nos possibilitar ver não somente um Equilíbrio de Nash na prática, mas nos mostra também uma nova configuração de jogo na qual os jogadores não estão escolhendo suas estratégias ao mesmo tempo, – jogos simultâneos – mas nesse caso há um jogador que teve a iniciativa para iniciar o jogo, com um primeiro movimento. Os primeiros são chamados de jogos simultâneos, e aqueles em que um jogador começa o jogo e em seguida o oponente responde são conhecidos como jogos na forma extensiva.
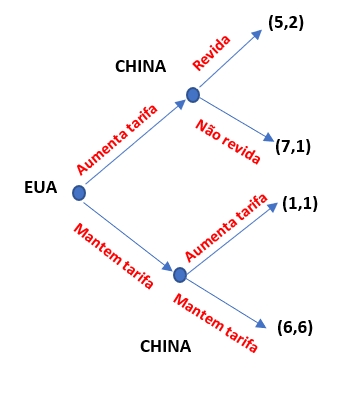
O jogo abaixo representa a interação estratégica no comércio exterior entre EUA e China na forma extensiva:
Como podemos observar, se os EUA aumentaram a tarifa de importação sobre os produtos chineses, a China pode revidar aumentando também suas tarifas de importação sobre produtos americanos, o que a faz obter um saldo em sua balança comercial de US$ 2 bilhões, enquanto os EUA obtém um saldo de US$ 5 bilhões; se não revidar, a China passa a ter um saldo de US$ 1 bilhão; por outro lado, caso os EUA mantenham a mesma tarifa de importação sobre os produtos da China, e essa aumenta a sua tarifa sobre os produtos americanos, o ganho dos dois na balança comercial passa a ser de US$ 1 bilhão; e, por último, quando nenhum dos dois países alterar suas tarifas, os ganhos são de US$ 6 bilhões para cada um. Se esse jogo estivesse representado na forma simultânea, teríamos a seguinte configuração:
No jogo simultâneo, os EUA e a China podem vislumbrar as duas possibilidades para o Equilíbrio de Nash, – que consiste em escolher uma estratégia em que se faz exatamente o que o adversário está fazendo. Contudo, no jogo na forma extensiva, uma vez que os EUA tenham tomado a iniciativa de adotar uma política protecionista, não cabe a China adotar outra estratégia que não seja a da retaliação[3].
Como você pode ver neste artigo, a Teoria dos Jogos possui diversas aplicações, sendo uma importante ferramenta de análise de situações de interação estratégica, não importando se os participantes do jogo sejam empresas de pequeno ou grande porte, economias de grandes países, ou mesmo prisioneiros incomunicáveis. Há sempre a possibilidade de aplicação desse conhecimento em um mercado cada vez mais complexo e competitivo.
Teoria dos Jogos – Quer obter mais conhecimento sobre? ou tem interesse em realizar um curso nessa área? Clique aqui! Estamos buscando quórum para formar um curso nessa área.
Referências
[1] O Dilema foi originalmente formulado por Merrill Flood e Melvin Dresher, em 1950. Posteriormente, Albert W. Tucker formalizou o problema, com o tema da pena de prisão, e o chamou pelo nome que conhecemos hoje.
[2] A descrição desse arranjo nos remete aos fatos da atualidade, em que indiciados na Operação Lava Jato aceitam confessar suas participações nos esquemas de corrupção. A chamada delação premiada não se limita à participação do confessor, mas também a de outros envolvidos. A redução da pena é a grande moeda de troca utilizada para incentivar os réus a confessar, mas diferentemente do Dilema do Prisioneiros, aqui existe a possibilidade de um acordo entre os indiciados.
[3] Desde Adam Smith e David Ricardo, com o conceito de vantagens comparativas, tem se demonstrado que a adoção de políticas protecionistas não é benéfica a nenhuma economia. Se um país produz um determinado produto com melhores preços, fechar a economia a esse produto sob o argumento de estar defendendo os empregos locais é na verdade uma forma de transferir o ônus daquela proteção comercial aos consumidores, que estão agora pagando um preço mais caro por um produto de qualidade similar.